1593. Элегантно
переставленная сумма
Задана последовательность из n целых чисел {a1, a2,
…, an}. Необходимо найти
такую ее перестановку, для которой сумма модулей разниц всех соседних элементов
максимальна. Эту наибольшую сумму будем называть элегантной.
Рассмотрим, например,
последовательность {4, 2, 1, 5}. Искомой является перестановка {2, 5, 1, 4}, а
ее элегантная сумма равна |2 – 5| + |5 – 1| + |1 – 4| = 3 + 4 + 3 = 10. Для
всех других 24 перестановок значение элегантной суммы не больше 10.
Вход. Первая строка содержит количество
тестов t (t < 100). Каждая следующая строка является отдельным тестом.
Каждая входная строка начинается числом n
(1 < n < 51), за которым
следует последовательность из n неотрицательных чисел. Каждое число в последовательности не более 1000.
Выход. Для
каждого теста вывести его номер и значение элегантной суммы.
|
Пример входа |
Пример выхода |
|
3 4
4 2 1 5 4
1 1 1 1 2 10 1 |
Case
1: 10 Case
2: 0 Case 3: 9 |
РЕШЕНИЕ
жадный
алгоритм
Анализ алгоритма
Отсортируем
числа входной последовательности a. Создадим новый массив v, в котором будем строить искомую
перестановку. Изначально занесем в него минимальный и максимальный элементы
последовательности a (и соответственно эти элементы удалим из а). Элегантную сумму будем подсчитывать в переменной s. Сначала положим s = | v[0] – v[1] |.
Пока массив a
не пустой, жадным методом делаем наилучший выбор среди следующих четырех
возможностей:
1.
Наименьший элемент текущего массива а ставим в начало массива v.
2.
Наименьший элемент текущего массива а ставим в конец массива v.
3.
Наибольший элемент текущего массива а ставим в начало массива v.
4.
Наибольший элемент текущего массива а ставим в конец массива v.
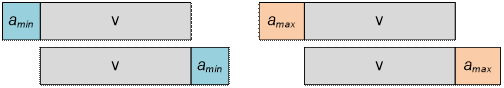
Для каждого
случая пересчитываем новое значение s.
Совершаем тот выбор, для которого новое значение s будет наибольшим. Для каждого теста в качестве ответа выводим
значение s.
Поскольку
массивы a и v обновляются динамически, в качестве контейнеров будем
использовать двусторонние очереди.
Пример
Рассмотрим работу алгоритма на
первом тесте. Отсортируем массив:
a = {1, 2, 4,
5}
Шаг 1. Занесем в массив v наименьший и наибольший элементы: v = {1, 5}. Удалим их из
a, после чего a = {2, 4}.
Наименьший
и наибольший элементы массива а
приписываем справа и слева от массива v. Наибольшее значение суммы
достигается, например, на массиве {1, 5, 2}.
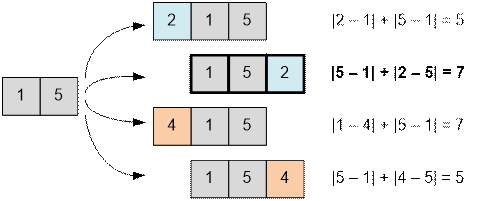
Шаг 2. v = {1, 5, 2}, a = {4}. В массиве a остался один
элемент. Приписываем его справа и слева от массива v. Пересчитываем суммы.

Искомая сумма равна 10,
достигается она например на перестановке
{4, 1, 5, 2}
Реализация алгоритма
Объявим рабочие очереди.
deque<int> a, v;
Читаем количество тестов tests.
scanf("%d", &tests);
for (i = 1; i <= tests; i++)
{
Начинаем обработку следующего
теста. Чистим содержимое массивов.
scanf("%d", &n);
a.clear();
v.clear();
Читаем входной массив а.
for (j = 0; j <
n; j++)
{
scanf("%d", &val);
a.push_back(val);
}
Сортируем входной массив.
sort(a.begin(),
a.end());
Заносим минимальный и
максимальный элементы последовательности a в массив v.
v.push_back(a.back());
v.push_front(a.front());
Положим изначально s = | v[1] – v[0] |.
s = abs(v.back()
- v.front());
Удаляем эти два элемента из
массива а.
a.pop_back();
a.pop_front();
Пока массив а не пустой, рассматриваем 4 случая и делаем среди них оптимальный
выбор жадным методом.
while (!a.empty())
{
Объявим целочисленный массив mx из четырех элементов.
mx[0] =
abs(v.front() - a.front());
mx[1] =
abs(v.back() - a.front());
mx[2] =
abs(v.front() - a.back());
mx[3] =
abs(v.back() - a.back());
rmax =
*max_element(mx, mx + 4);
if (rmax == mx[0])
{
v.push_front(a.front());
a.pop_front();
} else
if (rmax == mx[1])
{
v.push_back(a.front());
a.pop_front();
} else
if (rmax == mx[2])
{
v.push_front(a.back());
a.pop_back();
} else
{
v.push_back(a.back());
a.pop_back();
}
s += rmax;
}
Выводим ответ.
printf("Case %d:
%d\n", i, s);
}